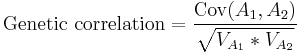Quantitative genetics
| Part of a series on |
| Genetics |
| Key components |
|---|
|
Chromosome |
| History and topics |
|
Evolution • Molecular |
| Research |
|
DNA sequencing |
| Biology portal • |
Quantitative genetics is the study of continuous traits (such as height or weight) and their underlying mechanisms. It is effectively an extension of simple Mendelian inheritance in that the combined effects of one or more genes and the environments in which they are expressed give rise to continuous distributions of phenotypic values.
Contents |
History
The field was founded, in evolutionary terms, by the originators of the modern synthesis, R.A. Fisher, Sewall Wright and J. B. S. Haldane, and aimed to predict the response to selection given data on the phenotype and relationships of individuals.
Analysis of Quantitative Trait Loci, or QTL, is a more recent addition to the study of quantitative genetics. A QTL is a region in the genome that affects the trait or traits of interest. Quantitative trait loci approaches require accurate phenotypic, pedigree and genotypic data from a large number of individuals.
Basic principles
The phenotypic value (P) of an individual is the combined effect of the genotypic value (G) and the environmental deviation (E):
- P = G + E
The genotypic value is the combined effect of all the genetic effects, including nuclear genes, mitochondrial genes and interactions between the genes. It is worthwhile to note that the mathematics is related to the genetics: for which the brief following revision may be useful. In disomic (diploid) organisms, a nucleus gene is represented twice in the gene-set ("genotype"), one contribution being provided by each parent during sexual reproduction. Each "gene" is located at a particular place (a "locus" - the Latin word for place; plural "loci") on corresponding chromosomes (homologues), one from each parent. Any gene may have several functional forms in the species as a whole, and each of these may lead to outwardly different "effects" (= an average result in the phenotype considered over a large sample of gene-backgrounds and environments). These functional forms are "alleles" (or "allelomorphs", the original term). If both alleles at a gene have the same phenotypic effect (are the "same"), the gene is said to be "homozygous": if each allele at a gene is different in effect, the gene is "heterozygous". The average phenotypic outcome may also depend upon how alleles interact with their own homologous partner in the disomic genotype ("dominance"), and on how these alleles interact with those of other genes at other loci which also affect this phenotypic trait ("epistasis"). Notice that we have combined classical genetics ideas with those of statistics in this exposition. Terms such as "gene", "homologue", "allele", "homozygous" and "heterozygous" are genetical: but "effect" is statistical, and refers to the average observed over an infinity of backgrounds, both genetical and environmental. Thus, we have very sneakily defined the "genetic value" (or "genotypic" value) as the infinity mean of all the phenotypes it can ever produce in time and space! Before molecular genetics, there simply was no other way to do it! And after molecular genetics, this is still the most utilitarian way to tackle the idea of genetic value! Also notice that we have openly used fundamentals of reproductive biology behind the genetics. The founder of Quantitative Genetics - Sir Ronald Fisher - perceived all of this when he proposed the first mathematics of this branch of Genetics [Fisher R.A. (1930). The Genetical theory of Natural Selection. Oxford Clarendon Press.]. He sought to define a single statistical summary of all the variance arising from phenotypic change during the course of genetical assortment and segregation, which he called the "genetic" variance. His residual genotypic variance (which he called simply the "residual") represented that part of assortment which did not lead to phenotypic change, although the genes themselves had in fact been subject to meiosis and syngamy, of course. [A simplified exposition of this can be found in Falconer and Mackay (1966) - see References.] These partitions subsequently became the familiar subdivisions of the "additive" (A) and "dominance" (D) variances, respectively. These later names are utterly misleading and very unfortunate, and have led to much confusion as to what they mean genetically. [It would have been better for posterity had they been named "Assortative" (A), and "Stable" (S).] A more gene-focused partitioning was invented by Mather and Jinks in 1971, but they also were statisticians rather than geneticists, had their own rather opaque symbolism, and became somewhat overwhelmed by the Fisherian approach. Added to all of this was the problem that Fisher's underlying reproduction model (mating system) was unrealistically simplistic: whilst it facilitated solving the equations, it didn't describe many real-life scenarios. Fortunately, Wright (in the 1950s) did provide the means to overcome complex mating systems, but its own complexity minimised its popular adoption. Early in this millennium [Heredity (2003) 91: 85-89], a comprehensive linking together of all of these approaches reconciled their various meanings and relationships (as well as correcting an error), and suggested that new partitions reflecting real homozygosis [a] and heterozygosis [d] should replace the present "additive" [A] and "dominance" [D] subdivisions. This paper revealed, by the way, that the Additive Genetical variance consists of all the homozygote variance, plus part of the dominance variance, and a frequency-weighted covariance between homozygote and heterozygote gene effects. The so-called Dominance variance contains only the remainder of the overall dominance variance of the gene in question, being therefore very misleading indeed! It should be understood, however, that either method of partitioning still accounts for all of the genotypic variance in the model being used: it's the way it has been divided up which is being debated. At least the Environmental variance is much more straight-forward. This can be subdivided into a pure environmental component (E) and an interaction component (I) describing the gene-environment interaction. The overall "single gene" model can be written as:
- P = a + d + E + I.
Expansion of the model to multiple genes (loci) is still not resolved satisfactorily, and until that is solved it is not possible to account for epistasis. The problem is being tackled currently. The contribution of those components cannot be determined in a single individual, but they can be estimated for whole populations by estimating the variances for those components, denoted as:
- VP = Va + Vd + VE + VI
The heritability of a trait is the proportion of the total (i.e. phenotypic) variance (VP) that is explained by the total genotypic variance (VG). This is known also as the "broad sense" heritability (H2). If only Additive genetic variance (VA) is used in the numerator, the heritability is "narrow sense" (h2). Unfortunately, this is often simply called "heritability", with little reflection about its true meaning. The broadsense heritability indicates the genotypic determination of the phenotype: while the latter estimates the degree of assortative disequlibrium in the trait. Fisher proposed that this narrow-sense heritability might be appropriate in considering the results of natural selection, focusing as it does on disequilibrium: and it has been used also for predicting the results of artificial selection. This latter usage seems to be inappropriate, however, as breeders are interested in steering attributes towards new phenotypes (that is in utilising all the gene effects), rather than simply exploiting disequilibrium.
Resemblance between relatives
Central in estimating the variances for the various components is the principle of relatedness. A child has a father and a mother. Consequently, the child and father share 50% of their alleles, as do the child and the mother. However, the mother and father normally do not share alleles as a result of shared ancestors. Similarly, two full siblings share also on average 50% of the alleles with each other, while half siblings share only 25% of their alleles. This variation in relatedness can be used to estimate which proportion of the total phenotypic variance (VP) is explained by the above-mentioned components.
Although some genes have only an effect on a single trait, many genes have an effect on various traits. Because of this, a change in a single gene will have an effect on all those traits. This is calculated using covariances, and the phenotypic covariance (CovP) between two traits can be partitioned in the same way as the variances described above. The genetic correlation is calculated by dividing the covariance between the additive genetic effects of two traits by the square root of the product of the variances for the additive genetic effects of the two traits:
See also
- Artificial selection
- Diallel cross
- Ewens's sampling formula
- Experimental evolution
- Genetic distance
- Heritability
- Population genetics, built on some of the same principles as quantitative genetics
- Selective breeding
References
- Falconer, D. S. & Mackay TFC (1996). Introduction to Quantitative Genetics. Fourth edition. Addison Wesley Longman, Harlow, Essex, UK.
- Roff DA (1997). Evolutionary Quantitative Genetics. Chapman & Hall, New York.
- Lynch M & Walsh B (1998). Genetics and Analysis of Quantitative Traits. Sinauer, Sunderland, MA.
- Gordon I.L. (2003). Refinements to the partitioning of the inbred genotypic variance. Heredity 91: 85-89.
- Fisher R.A. (1930). The Genetical Theory of Natural Selection. Clarendon Press, Oxford, UK.
- Mather K. & Jinks J.L. (1971). Biometrical Genetics. Chapman & Hall, London.
- Wright S. (1951). The genetical structure of populations. Annals of Eugenics 15: 323-354.
External links
- Quantitative Genetics Resources by Michael Lynch and Bruce Walsh, including the two volumes of their textbook, Genetics and Analysis of Quantitative Traits and Evolution and Selection of Quantitative Traits.
- Resources by Nick Barton et al. from the textbook, Evolution.
|
||||||||||
|
|||||||||||||||||